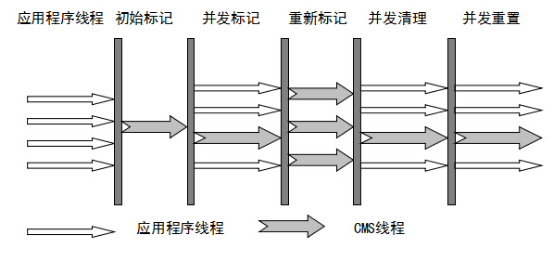
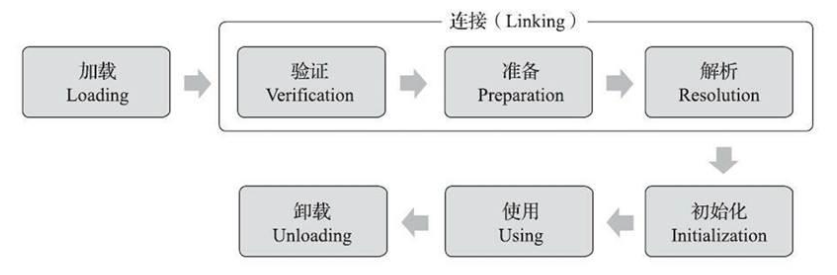
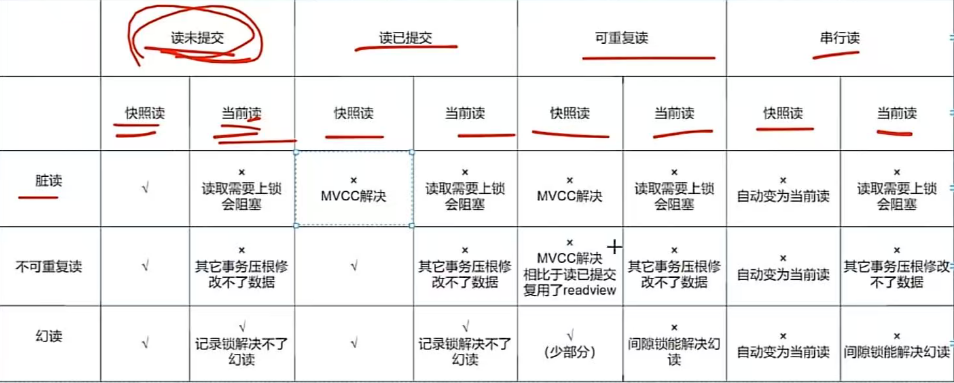
题解

P10389（洛谷题面） 题目 题目描述： 小蓝的班上有 nnn 个人，一次考试之后小蓝想统计同学们的成绩，第 iii 名同学的成绩为 aia_iai​。当小蓝统计完前 xxx 名同学的成绩后，他可以从 1∼x1 \sim x1∼x 中选出任意 kkk 名同学的成绩，计算出这 kkk 个成绩的方差。小蓝至少要检查多少个人的成 绩，才有可能选出 kkk 名同学，他们的方差小于一个给定的值 TTT？ 提示：kkk 个数 v1,v2,⋯ ,vkv_1, v_2, \cdots , v_kv1​,v2​,⋯,vk​ 的方差 σ2\sigma^2σ2 定义为：σ2=∑i=1k(vi−vˉ)2k\sigma^2=\dfrac {\sum_{i=1}^k(v_i-\bar v)^2} kσ2=k∑i=1k​(vi​−vˉ)2​，其中 vˉ\bar vvˉ 表示 viv_ivi​ 的平均值，vˉ=∑i=1kvik\bar v = \dfrac {\sum_{i=1}^k v_i} kvˉ=k∑i=1k​vi​​。 输入格式： 输入的第一行包含三个正整数...

P1115 最大子段和（洛谷题面） 题目 题目描述： 给出一个长度为 nnn 的序列 aaa，选出其中连续且非空的一段使得这段和最大。 输入格式： 第一行是一个整数，表示序列的长度 nnn。 第二行有 nnn 个整数，第 iii 个整数表示序列的第 iii 个数字 aia_iai​。 输出格式： 输出一行一个整数表示答案。 数据范围与说明： 样例 1 解释 选取 [3,5][3, 5][3,5] 子段 {3,−1,2}\{3, -1, 2\}{3,−1,2}，其和为 444。 数据规模与约定 对于 40%40\%40% 的数据，保证 n≤2×103n \leq 2 \times 10^3n≤2×103。 对于 100%100\%100% 的数据，保证 1≤n≤2×1051 \leq n \leq 2 \times 10^51≤n≤2×105，−104≤ai≤104-10^4 \leq a_i \leq 10^4−104≤ai​≤104。 2026/01/21：增加一组 hack 数据。 输入输出样例 #1 输入： 1272 -4 3 -1 2 -4...

P1271 题目 题目描述： 学校正在选举学生会成员，有 nnn（1≤n≤9991 \le n\le 9991≤n≤999）名候选人，每名候选人编号分别从 111 到 nnn，现在收集到了 mmm（1≤m≤20000001 \le m \le 20000001≤m≤2000000）张选票，每张选票都写了一个候选人编号。现在想把这些堆积如山的选票按照投票数字从小到大排序。设第 iii（1≤i≤m1 \le i \le m1≤i≤m）张选票上的数字为 aia_iai​，则保证有 1≤ai≤n1 \le a_i \le n1≤ai​≤n。 输入格式： 输入 nnn 和 mmm 以及 mmm 个选票上的数字。 输出格式： 求出排序后的选票编号。 数据范围与说明： 输入输出样例 #1 输入： 125 102 5 2 2 5 2 2 2 1 2 输出： 11 2 2 2 2 2 2 2 5 5 代码 1234567891011#include <bits/stdc++.h>using namespace std;int n,m;int main(){ ...

P1806 题目 题目描述： 路人甲准备跑 nnn 圈来锻炼自己的身体，他准备分多次（>1\gt1>1）跑完，每次都跑正整数圈，然后休息下再继续跑。 为了有效地提高自己的体能，他决定每次跑的圈数都必须比上次跑的多。 可以假设他刚开始跑了 000 圈，那么请问他可以有多少种跑完这 nnn 圈的方案？ 输入格式： 一行一个整数，代表 nnn。 输出格式： 一个整数表示跑完这 nnn 圈的方案数。 数据范围与说明： 数据规模与约定 对于 100%100\%100% 的数据，保证 5≤n≤5005\le n\le 5005≤n≤500。 输入输出样例 #1 输入： 1212 输出： 1995645335 代码 123456789101112131415#include <bits/stdc++.h>using namespace std;int n;long long dp[505];int main(){ cin>>n; dp[0]=1; for(int i=1;i<=n;i++){ for(int...

P1419 题目 题目描述： 给定一个长度为 nnn 的序列 aaa，定义 aia_iai​ 为第 iii 个元素的价值。现在需要找出序列中最有价值的“段落”。段落的定义是长度在 [S,T][S, T][S,T] 之间的连续序列。最有价值段落是指平均值最大的段落。 段落的平均值 等于 段落总价值 除以 段落长度。 输入格式： 第一行一个整数 nnn，表示序列长度。 第二行两个整数 SSS 和 TTT，表示段落长度的范围，在 [S,T][S, T][S,T] 之间。 第三行到第 n+2n+2n+2 行，每行一个整数表示每个元素的价值指数。 输出格式： 一个实数，保留 333 位小数，表示最优段落的平均值。 数据范围与说明： 【数据范围】 对于 30%30\%30% 的数据有 n≤1000n \le 1000n≤1000。 对于 100%100\%100% 的数据有 1≤n≤1000001 \le n \le 1000001≤n≤100000，1≤S≤T≤n1 \le S \le T \le n1≤S≤T≤n，−104≤ai≤104-{10}^4 \le a_i \le...

P10903（洛谷题面） 题目 题目描述： 在库存管理系统中，跟踪和调节商品库存量是关键任务之一。小蓝经营的仓库中存有多种商品，这些商品根据类别和规格被有序地分类并编号，编号范围从 111 至 nnn。初始时，每种商品的库存量均为 000。 为了高效地监控和调整库存量，小蓝的管理团队设计了 mmm 个操作，每个操作涉及到一个特定的商品区间，即一段连续的商品编号范围（例如区间 [L,R][L, R][L,R]）。执行这些操作时，区间内每种商品的库存量都将增加 111。然而，在某些情况下，管理团队可能会决定不执行某些操作，使得这些操作涉及的商品区间内的库存量不会发生改变，维持原有的状态。 现在，管理团队需要一个评估机制，来确定如果某个操作未被执行，那么最终会有多少种商品的库存量为 000。对此，请你为管理团队计算出，对于每个操作，如果不执行该操作而执行其它操作，库存量为 000 的商品的种类数。 输入格式： 输入的第一行包含两个整数 nnn 和 mmm，分别表示商品的种类数和操作的个数。 接下来的 mmm 行，每行包含两个整数 LLL 和...

P2249 【深基13.例1】查找（洛谷题面） 题目 题目描述： 输入 nnn 个不超过 10910^9109 的单调不减的（就是后面的数字不小于前面的数字）非负整数 a1,a2,…,ana_1,a_2,\dots,a_{n}a1​,a2​,…,an​，然后进行 mmm 次询问。对于每次询问，给出一个整数 qqq，要求输出这个数字在序列中第一次出现的编号，如果没有找到的话输出 −1-1−1 。 输入格式： 第一行 222 个整数 nnn 和 mmm，表示数字个数和询问次数。 第二行 nnn 个整数，表示这些待查询的数字。 第三行 mmm 个整数，表示询问这些数字的编号，从 111 开始编号。 输出格式： 输出一行，mmm 个整数，以空格隔开，表示答案。 数据范围与说明： 数据保证，1≤n≤1061 \leq n \leq 10^61≤n≤106，0≤ai,q≤1090 \leq a_i,q \leq 10^90≤ai​,q≤109，1≤m≤1051 \leq m \leq 10^51≤m≤105 本题输入输出量较大，请使用较快的 IO 方式。 输入输出样例...

P1873 题目 题目描述： 伐木工人 Mirko 需要砍 MMM 米长的木材。对 Mirko 来说这是很简单的工作，因为他有一个漂亮的新伐木机，可以如野火一般砍伐森林。不过，Mirko 只被允许砍伐一排树。 Mirko 的伐木机工作流程如下：Mirko 设置一个高度参数 HHH（米），伐木机升起一个巨大的锯片到高度 HHH，并锯掉所有树比 HHH 高的部分（当然，树木不高于 HHH 米的部分保持不变）。Mirko 就得到树木被锯下的部分。例如，如果一排树的高度分别为 20,15,1020,15,1020,15,10 和 171717，Mirko 把锯片升到 151515 米的高度，切割后树木剩下的高度将是 15,15,1015,15,1015,15,10 和 151515，而 Mirko 将从第 111 棵树得到 555 米，从第 444 棵树得到 222 米，共得到 777 米木材。 Mirko 非常关注生态保护，所以他不会砍掉过多的木材。这也是他尽可能高地设定伐木机锯片的原因。请帮助 Mirko 找到伐木机锯片的最大的整数高度 HHH，使得他能得到的木材至少为 MMM...

P10424（洛谷题面） 题目 题目描述： 一个整数如果按从低位到高位的顺序，奇数位（个位、百位、万位……）上的数字是奇数，偶数位（十位、千位、十万位……）上的数字是偶数，我们就称之为“好数”。 给定一个正整数 NNN，请计算从 111 到 NNN 一共有多少个好数。 输入格式： 一个整数 NNN。 输出格式： 一个整数代表答案。 数据范围与说明： 样例 1 解释 242424 以内的好数有 1,3,5,7,9,21,231,3,5,7,9,21,231,3,5,7,9,21,23，一共 777 个。 数据规模与约定 对于 10%10\%10% 的测试数据，1≤N≤1001 \leq N \le 1001≤N≤100。 对于全部的测试数据，1≤N≤1071 \le N \leq 10^71≤N≤107。 输入输出样例 #1 输入： 124 输出： 17 输入输出样例 #2 输入： 12024 输出： 1150 ...

P1017 [NOIP 2000 提高组] 进制转换（洛谷题面） 题目 题目描述： 我们可以用这样的方式来表示一个十进制数：将每个阿拉伯数字乘以一个以该数字所处位置为指数，以 101010 为底数的幂之和的形式。例如 123123123 可表示为 1×102+2×101+3×1001 \times 10^2+2\times 10^1+3\times 10^01×102+2×101+3×100 这样的形式。 与之相似的，对二进制数来说，也可表示成每个二进制数码乘以一个以该数字所处位置为指数，以 222 为底数的幂之和的形式。 一般说来，任何一个正整数 RRR 或一个负整数 −R-R−R 都可以被选来作为一个数制系统的基数。如果是以 RRR 或 −R-R−R 为基数，则需要用到的数码为 0,1,…,R−10,1,\dots,R-10,1,…,R−1。 例如当 R=7R=7R=7 时,所需用到的数码是 0,1,2,3,4,5,60,1,2,3,4,5,60,1,2,3,4,5,6，这与其是 RRR 或 −R-R−R 无关。如果作为基数的数绝对值超过...